You signed in with another tab or window. Reload to refresh your session.You signed out in another tab or window. Reload to refresh your session.You switched accounts on another tab or window. Reload to refresh your session.Dismiss alert
| <ahref="https://colab.research.google.com/github/VincentStimper/normalizing-flows/blob/master/examples/real_nvp_colab.ipynb"target="_parent"><imgsrc="https://colab.research.google.com/assets/colab-badge.svg"alt="Open In Colab"/></a> | Real NVP applied to a 2D bimodal target distribution |
29
+
| <ahref="https://colab.research.google.com/github/VincentStimper/normalizing-flows/blob/master/examples/paper_example_nsf_colab.ipynb"target="_parent"><imgsrc="https://colab.research.google.com/assets/colab-badge.svg"alt="Open In Colab"/></a> | Modeling a distribution on a cylinder surface with a neural spline flow |
19
30
20
31
21
32
## Implemented Flows
@@ -153,7 +164,7 @@ Note that there might be a density filament connecting the two modes, which is d
153
164
of normalizing flows, especially prominent in Real NVP. You can find out more about it in
### Modeling a distribution on a cylinder surface with a neural spline flow
157
168
158
169
<ahref="https://colab.research.google.com/github/VincentStimper/normalizing-flows/blob/master/examples/paper_example_nsf_colab.ipynb"target="_parent"><imgsrc="https://colab.research.google.com/assets/colab-badge.svg"alt="Open In Colab"/></a>
159
170
@@ -163,7 +174,7 @@ as well, we apply a Neural Spline Flow model to a distribution defined on a cyli
163
174
164
175
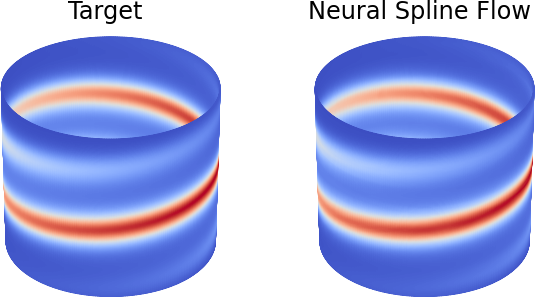
165
176
166
-
This example is considered in the [paper](https://github.com/VincentStimper/normalizing-flows/blob/master/paper/paper.md) accompanying this repository.
177
+
This example is considered in the [paper](https://arxiv.org/abs/2302.12014) accompanying this repository.
167
178
168
179
## Used by
169
180
@@ -192,20 +203,19 @@ has been build upon `normflows`.
192
203
193
204
## Citation
194
205
195
-
If you use `normflows`, please consider citing it as follows.
206
+
If you use `normflows`, please consider citing the [corresponding paper](https://arxiv.org/abs/2302.12014) as follows.
196
207
197
-
> Vincent Stimper, David Liu, Andrew Campbell, Vincent Berenz, Lukas Ryll, Bernhard Schölkopf, José Miguel Hernández-Lobato:
198
-
> normflows: A PyTorch Package for Normalizing Flows,
> Vincent Stimper, David Liu, Andrew Campbell, Vincent Berenz, Lukas Ryll, Bernhard Schölkopf, José Miguel Hernández-Lobato.
209
+
> normflows: A PyTorch Package for Normalizing Flows, arXiv preprint arXiv:2302.12014, 2023.
200
210
201
211
**Bibtex**
202
212
203
213
```
204
-
@software{normflows,
214
+
@article{normflows,
205
215
author = {Vincent Stimper and David Liu and Andrew Campbell and Vincent Berenz and Lukas Ryll and Bernhard Sch{\"o}lkopf and Jos{\'e} Miguel Hern{\'a}ndez-Lobato},
206
216
title = {normflows: {A} {P}y{T}orch {P}ackage for {N}ormalizing {F}lows},
Copy file name to clipboardExpand all lines: examples/paper_example_nsf_colab.ipynb
+3-1Lines changed: 3 additions & 1 deletion
Original file line number
Diff line number
Diff line change
@@ -21,7 +21,9 @@
21
21
"id": "a3f13738",
22
22
"metadata": {},
23
23
"source": [
24
-
"We aim to approximate a distribution having as circular and a normal coordinate. To construct such a case, let $x$ be the normal (unbound) coordinate follow a standard normal distribution, i.e. \n",
24
+
"This is the example we consider in our [paper](https://arxiv.org/abs/2302.12014) about the `normflows` package.\n",
25
+
"\n",
26
+
"We aim to approximate a distribution having as circular and a normal coordinate. To construct such a case, let $x$ be the normal (unbound) coordinate follow a standard normal distribution, i.e.\n",
25
27
"$$ p(x) = \\frac{1}{\\sqrt{2\\pi}} e^{-\\frac{1}{2} x ^ 2}.$$\n",
26
28
"The circular random variable $\\phi$ follows a [von Mises distribution](https://en.wikipedia.org/wiki/Von_Mises_distribution) given by\n",
0 commit comments