Arc, tangents & Bezier studies

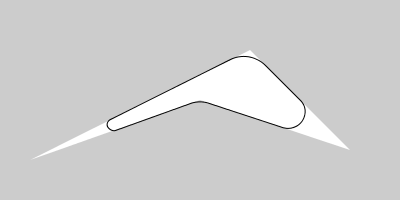
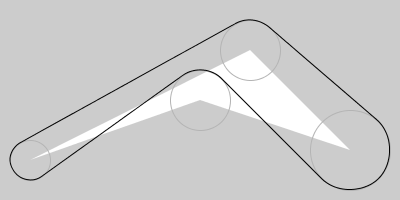
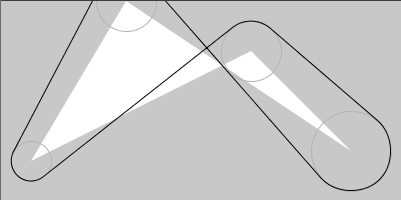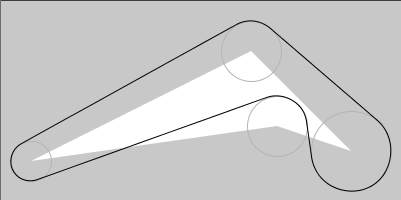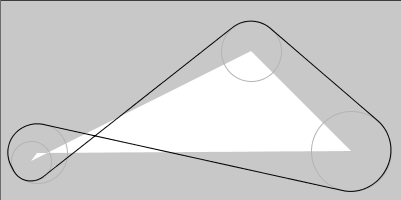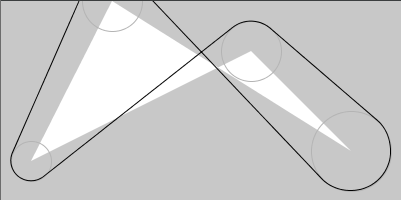
from sketch-a-day project, sketch_2020_09_26a

This repository contains the product of my studies trying to work with arcs, bezier approximations of arcs and tangents. I have added just a few new ideas here, you can look at the findings & previous studies I moved into the PRIOR_ART folder, and I tried to attribute stuff with links. Feel free to open an issue if you have a question.

The functions presented here can be found at arcs.py, they were made initially on Processing Python mode and now work with py5. Most will work with pyp5js or with the modified pyp5js/py5mode too, and I have ported b_arc for Processing Java and p5js.

You are welcome to help porting more stuff!

Please note that the most recent (and maybe unstable?) version of the Python functions shown here, with support only for py5, are kept at this other repository: github.com/villares/villares, on arcs_helper.py.

Consider supporting my work with a small donation (links on the footer).

Bezier approximation of an arc

Processing PShape insfrastructure and py5's Py5Shape, that depends on it, do not contain fuctions for embeding an arc in a larger polyline shape. The b_arc function provided here can be used inside begin_shape()/end_shape() as a kind of "arc_vertex" (which doesn't exist). It follows mostly the Processing/py5 arc signature, but does not include PIE and CHORD modes. You can find demos at:

• b_arc for py5, also works on pyp5js/py5mode on your browser

• b_arc the legacy Processing Python mode version, works on unmodified pyp5js

• b_arc for Processing Java

• b_arc for p5.js

  

x, y, w, h, start_angle, end_angle = 75, 100, 100, 100, 0, PI + QUARTER_PI
# Standalone arc replacement
b_arc(x, y, w, h, start_angle, end_angle)

# mode=2 for use inside begin_shape/end_shape
x += 125
begin_shape()
b_arc(x, y, w, h, start_angle, end_angle, mode=2) 
end_shape(CLOSE)
x += 125
begin_shape()
b_arc(x, y, w, h, start_angle, end_angle, mode=2)
vertex(x, y)
end_shape(CLOSE)

More arcs, the p_arc function, and the first shapes with tangents

Other functions based on b_arc, and a polygonal approximation called p_arc can be found on arcs.py and arc_helpers.py:

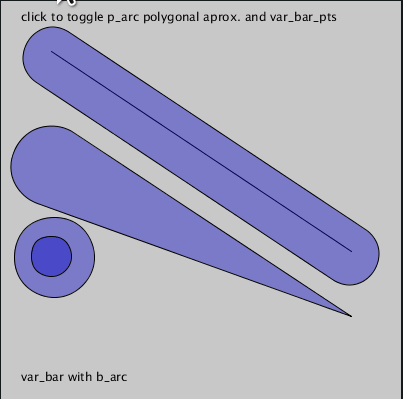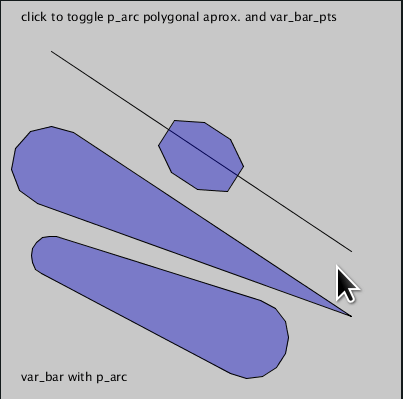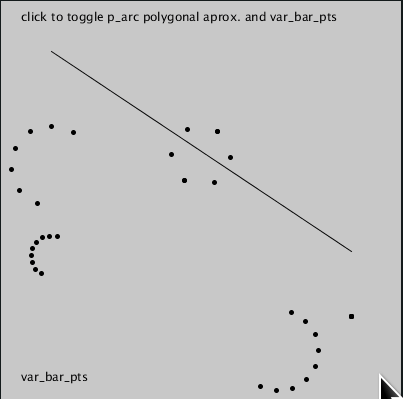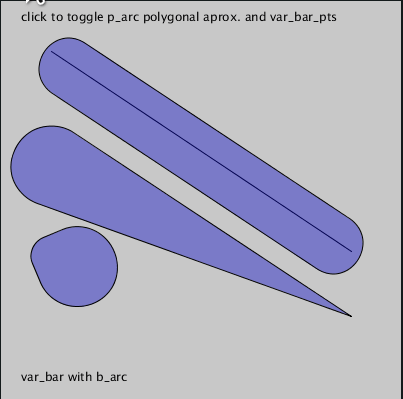
• The var_bar and bar functions draw "two connected circles". They can be used with p_arc(a polygonal approximation of an arc) instead of the default b_arc.

• The var_bar_pts function, based on arc_pts, returns the points that var_bar would draw with the same arguments (except the internal feature).

• The arc_pts function returns a list of points (as tuples), that p_arc would draw, but does not draw them. p_arc now uses arc_pts internally.

…
# default var_bar & bar with b_arc
var_bar(50, 165, 350, 315, 40, 0) # by default arc_func=b_arc
bar(50, 55, 350, 255, thickness=60, shorter=mouse_x)
var_bar(50, 255, 50 + mouse_x * 0.6, 255 + mouse_x * 0.25, 20, 40)
… 
# var_bar & bar with p_arc
var_bar(50, 165, 350, 315, 40, 0, arc_func=p_arc, num_points=6)
bar(50, 55, 350, 255, thickness=60,
    shorter=mouse_x, arc_func=p_arc, num_points=3)
var_bar(50, 255,
        50 + mouse_x * 0.6, 255 + mouse_x * 0.25, 20, 40,
        arc_func=p_arc, num_points=8)
… 
# var_bar_pts
pts1 = var_bar_pts(50, 165, 350, 315, 40, 0, num_points=6)
pts2 = var_bar_pts(50, 55, 350, 255, 30, 30,
                   shorter=mouse_x, num_points=3)
pts3 = var_bar_pts(50, 255,
                   50 + mouse_x * 0.6, 255 + mouse_x * 0.25, 20, 40,
                   num_points=8)
stroke_weight(5)
for px, py in pts1 + pts2 + pts3:
    point(px, py)
…

The full code for this interactive demo can be found here and it also runs on the browser with pyp5js/py5mode here!

Filleted polygons and nice shapes that can wrap circles

Perhaps the bigest motivation for starting the studies in this repository, next, we have some functions that povide continous poly-based shapes with tangent arcs.

• Rounding polygons "in", filleted polygons arc_filleted_poly, takes a sequence of points and radii and uses the arc_cornerfunction to draw. Notice it may need to make a radius smaller to fit sometimes. A recently added radius keyword can be supplied instead of the radius values list.

  

  p_list = [(30, 160), (250, 50), (350, 150), (200, 100)]
  r_list = [20, 30, 40, 30]
  …
  arc_filleted_poly(p_list,r_list)  # arc_func=b_arc by default

  

  p_list = [(30, 160), (250, 50), (350, 150), (mouse_x, mouse_y)]
  r_list = [20, 30, 40, 30]
  …
  arc_filleted_poly(p_list,r_list)  # arc_func=b_arc by default

• Rounding polygons "outside" with arc_augmented_poly, takes a sequence of points and radii and calculates geometry with the circ_circ_tangent function. If two points are too close it will reduce the radii.

  

  p_list = [(30, 160), (250, 50), (350, 150), (200, 100)]
  r_list = [20, 30, 40, 30]
  …
  arc_augmented_poly(p_list,r_list)  # arc_func=b_arc by default

  

  p_list = [(30, 160), (250, 50), (350, 150), (mouse_x, mouse_y)]
  r_list = [20, 30, 40, 30]
  …
  arc_augmented_poly(p_list,r_list)  # arc_func=b_arc by default

  • TO DO: I should document an "ugly" feature of arc_augmented_poly that checks for self intersections calculating a polygonal approximation, without drawing the shapes.

  A few other silly arc helpers

• The circle_arc function tries to create a simpler interface for Processing's arc, asking for x, y, radius, start_angle, and sweep (radius instead of width, height and sweep instead of end_angle). It also allows drawing with b_arc or p_arc.

• The half_circle and quarter_circle are similar, very silly arc (or b_arc/p_arc) wrappers using a mix of Processing constants to define rotation.

  

  x, y, radius, start_angle, sweep = 75, 105, 50, 0, PI + QUARTER_PI
  circle_arc(x, y, radius, start_angle, sweep)    # default 'arc' wrapper mode
  circle_arc(x, y, radius, -QUARTER_PI / 2, -HALF_PI, arc_func=p_arc, num_points=4)
  
  x, y1, y2 = 190, 95, 105
  half_circle(x, y1, radius, TOP, CHORD)  # default 'arc' wrapper mode
  half_circle(x, y2, radius, BOTTOM, arc_func=b_arc)
  
  x1, x2, y1, y2 = 300, 310, 95, 105
  quarter_circle(x1, y1, radius, TOP + LEFT, CHORD)  # default 'arc' wrapper mode
  quarter_circle(x1, y2, radius, BOTTOM + LEFT, PIE)
  quarter_circle(x2, y1, radius, TOP + RIGHT)
  quarter_circle(x2, y2, radius, BOTTOM + RIGHT, arc_func=b_arc)

• circle_arc_pts will return a list of points like the ones p_arc would draw.

---

If you like this, support my work with a small donation! Here, with Wise or at LiberaPay.